Pengertian Integral

1.1. Konsep Integral

Sebelumnya kita telah mempelajari konsep turunan, karena konsep turunan sangat berhubungan dengan konsep integral yang akan kita pelajari. Bagaimanakah hubungan konsep turunan dan konsep integral?

Pada pembahasan turunan fungsi, telah dipelajari operasi pendiferensialan, yaitu proses menentukan turunan suatu fungsi, misalkan fungsi $F'(x) = f(x)$, dengan $f(x)$ turunan dari fungsi $F(x)$.

Hubungan tersebut biasa ditulis dengan $F'(x) = \frac {dF(x)}{dx} = f(x)$

Sekarang, dapatkah kita menentukan fungsi $F(x)$ dari $F'(x)$ yang diketahui?Untuk menentukannya invers/kebalikan dari operasi pendiferensialan atau operasi antiturunan yang lazim disebut dengan operasi pengintegralan.Operasi pengintegralan dinotasikan dengan $\int$.Misalnya, pengintegralan dari fungsi $F'(x) = f(x)$ terhadap variable $x$ dalam notasi integral ditulis sebagai berikut.

$\int{f(x)}dx$ (dibaca "integral $f(x)$ terhadap $x$")

Mari Mengamati 1

Tentukan turunan fungsi-fungsi berikut.

Dapatkah kamu tentukan turunan fungsi-fungsi tersebut? Coba kamu turunkan fungsi-fungsi tersebut kemudian amatilah turunan nilai konstantanya! Hubungkan kembali fungsi awal dengan turunannya serta anti turunannya! (petunjuk: turunan fungsi $F(x)$ adalah $F'(x) = f(x) =y'$)

#	Soal	Penyelesaian:	Hasil
1.	$F(x) = \frac{1}{4}x^4$	$F'(x)=f(x)=y'$=$\frac{d}{dx}[\frac{1}{4}x^4]=$ $\frac{1}{4}.4x^{4-1}=\frac{4}{4}x^{3}$	$x^3$
2.	$F(x) = \frac{1}{4}x^4 + 4$	$F'(x)=f(x)=y'$=$\frac{d}{dx}[\frac{1}{4}x^4 + 4]=$ $\frac{1}{4}.4x^{4-1} + 0 =\frac{4}{4}x^{3}$	$x^3$
3.	$F(x) = \frac{1}{4}x^4 - \frac{1}{2}$	$F'(x)=f(x)=y'$=$\frac{d}{dx}[\frac{1}{4}x^4 - \frac{1}{2}]=$ $\frac{1}{4}.4x^{4-1} + 0 =\frac{4}{4}x^{3}$	$x^{3}$

Berdasarkan pengamatan diatas dapat diklasifikasikan bahwa $f(x) = x^3$ merupakan turunan dari $F(x) = \frac{1}{4} x^4$, sehingga, $F(x) = \frac{1}{4} x^4$ merupakan antiturunan dari $f(x) = x^3$. Jadi, dapat ditunjukkan bahwa sebuah fungsi dapat memiliki banyak antiturunan dengan konstanta yang berbeda.

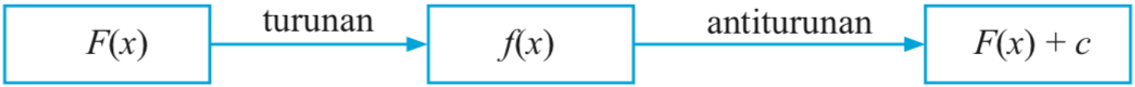
Anti turunan suatu fungsi dapat digambarkan seperti diagram dibawah ini: diagram

Secara induktif dapat diambil kesimpulan bahwa jika $F(x)$ adalah fungsi yang dapat diturunkan, yaitu $f(x)$ maka antiturunan dari $f(x)$ adalah $F(x) + c$ dengan $c$ adalah sembarang konstanta. Berdasarkan pemaparan tersebut dapat disimpulkan pengertian Integral (antiturunan) yaitu:

*Agar lebih memahami mari perhatikan contoh soal di halaman selanjutnya!

Contoh soal

Carilah antiturunan berikut:

$1$. $y' = \frac {dy}{dx} = x^4 $

Penyelesaian:

$y' = \frac {dy}{dx} = x^4 $,

Turunan dari $x^5$ pastilah mengandung unsur $x^4$ sehingga
$ \frac{d}{dx}(x^5) = 5x^4$
Supaya koefisiennya menjadi $1$ maka kedua ruas dapat dikali dengan $\frac{1}{5}$ menjadi:
$\frac{d}{x}(\frac{1}{5}x^5) = \frac{1}{5}.5x^4$ sehingga $\frac{d}{dx}(\frac{1}{5}x^5) = x^4 $

Jadi antiturunan $y'=\frac{dy}{dx} = x^4$ adalah $y=\frac{1}{5}x^5$

Langkah 1

$2$. $y' = \frac {dy}{dx} = 2x^3 $

Penyelesaian:

$y' = \frac {dy}{dx} = 2x^3 $,

Turunan dari $x^4$ pastilah mengandung unsur $x^3$ sehingga
$\frac{d}{dx}(x^4) = 4x^3$
Supaya koefisiennya menjadi $1$ maka kedua ruas dapat dikali dengan $\frac{1}{4}$ menjadi:
$\frac{d}{x}(\frac{1}{4}x^4) = \frac{1}{4}.4x^3$ sehingga $\frac{d}{dx}(\frac{1}{4}x^4) = x^3 $
Sekarang hasil antiturunan $x^3$ yaitu $\frac{1}{4}x^4$ kalikan dengan 2 menjadi:
$\frac{d}{dx}(2(\frac{1}{4}x^4)) = \frac{d}{dx}(\frac{2}{4}x^4) = \frac{d}{dx}(\frac{1}{2}x^4) = 2x^3 $

Jadi, antiturunan $y'= \frac{dy}{dx} = 2x^3$ adalah $\frac{1}{2}x^4$

Langkah 1

$3$. $y' = \frac {dy}{dx} = \frac{1}{\sqrt{x}} $

Penyelesaian:

$y' = \frac {dy}{dx} = \frac{1}{\sqrt{x}} $,

Ubah $\frac{dy}{dx} = \frac{1}{\sqrt{x}}$ menjadi bentuk perpangkatan biasa yaitu
$\frac{dy}{dx} = \frac{1}{\sqrt{x}} = x^{-\frac{1}{2}}$
Untuk mempermudah ambil fungsi yang pangkat satu lebih besar daripada $x^{-\frac{1}{2}}$ yaitu $x^{\frac{1}{2}}$
Turunkan fungsi $x^{\frac{1}{2}}$ sehingga
$\frac{d}{dx}(x^{\frac{1}{2}})$ = $\frac{1}{2}x^{-\frac{1}{2}}$
Supaya koefisiennya menjadi $1$ maka kedua ruas dapat dikali dengan $2$ menjadi:
$\frac{d}{dx}(2x^{\frac{1}{2}}) = 2.\frac{1}{2}x^{-\frac{1}{2}}$ sehingga $\frac{d}{dx}(2x^\frac{1}{2})$ = $x^{-\frac{1}{2}}$
Ubah hasil antiturunan $\frac{d}{dx}(2x^{\frac{1}{2}})$ ke bentuk akar menjadi:
$2\sqrt{x}$

Jadi, antiturunan dari $ y' = \frac{dy}{dx} = \frac{1}{\sqrt{x}} $ adalah $y = 2\sqrt{x}$

Langkah 1

Petunjuk

Isikan jawaban kamu pada kolom titik-titik atau kosong secara berurutan dari kiri ke kanan disetiap.
Gunakan angka saat memasukkan/megisikan jawaban
Jika jawaban kamu benar maka kolom tersebut akan berubah menjadi warna hijau.
Jika jawaban kamu salah maka kolom tersebut akan berubah menjadi warna merah.
Jika jawaban kamu salah, kamu dapat menghapus jawaban tersebut dan mengantinya dengan jawaban yang benar
Input disamping akan terisi jika jawaban anda benar atau salah

Mari Mencoba

1. Carilah antiturunan $y' = \frac {dy}{dx} = x^3 $

Penyelesaian:

Diketahui: $y' = \frac {dy}{dx} = x^3 $

Dijawab:

Turunan dari $x$ pastilah mengandung unsur $x^{3}$ sehingga
$\frac{d}{dx}$($x$ ) = $x$
Supaya koefisiennya menjadi $1$ maka kedua ruas dapat dikali dengan $\frac{1}{4}$ menjadi:
$\frac{d}{dx}$(
/
$x$ ) =
/
.$x$

Sehingga $\frac{d}{dx}$(
/
$x$) = $x^{3}$

Jadi, antiturunan $y'= \frac{dy}{dx} = x^3$ adalah $y = $

2.Carilah antiturunan $y' = \frac {dy}{dx} = 3x^5 $

Penyelesaian:

Diketahui: $y' = \frac {dy}{dx} = 3x^5 $

Dijawab:

Abaikan nilai koefisiennya terlebih dahulu
Turunan dari $x$ pastilah mengandung unsur $x^5$ sehingga
$\frac{d}{dx}$($x$) $=$ $x$

Supaya koefisiennya menjadi 1 maka kedua ruas dapat dikali dengan
/
menjadi:

$\frac{d}{dx}$(
/
$x$ ) $=$
/
. $x$

Sehingga $\frac{d}{dx}$ (
/
$x$) $=x^{5}$

Sekarang hasil antiturunan $x^5$ yaitu kalikan dengan menjadi:
$\frac{d}{dx}$( (

$x$)) $= \frac{d}{dx}$(

$x$) $= \frac{d}{dx}$(
/
$x$) = $3x^5$

Jadi, antituran $y'=\frac{dy}{dx} = 3x^{5}$ adalah $y = $

3. Carilah antiturunan $y' = \frac {dy}{dx} = \frac{5}{\sqrt{x}} $

Penyelesaian:

$y' = \frac {dy}{dx} = \frac{5}{\sqrt{x}} $

Ubah $\frac{dy}{dx}=\frac{5}{\sqrt{x}}$ menjadi perpangkatan biasa yaitu $\frac{dy}{dx} = $ $x$^{$-$^/}
Abaikan terlebih dahulu koefisiennya
ambil fungsi pangkat satu lebih besar daripada yaitu $x$^{^/}
Turunakan fungsi

$\frac{d}{dx}$($x$^{^/}) $=$

$x$ ^$-$

Supaya koefisiennya menjadi $1$ maka kedua ruas dikali menjadi:
$\frac{d}{dx}$($x$ ^/ ) $=$ .
/
$x$ ^{$-$^/}

Sehingga $\frac{d}{dx}$( $x$ ^{^/} ) $= x^{-\frac{1}{2}}$

Sekarang hasil antiturunan yaitu kalikan dengan

() = $x$ ^{^/}
Ubah hasil turunan $\frac{d}{dx} = $ ke bentuk akar menjandi:
√

Jadi, hasil anntiturunan dari $y'=\frac{d}{dx}=\frac{5}{\sqrt{x}} $ adalah $y = $